Worum geht es in diesem Artikel?
In der Welt der Maschinen und Technik sind Vibrationen ein allgegenwärtiges Phänomen und für Schwingungsexperten auch „faszinierend“. In diesem Artikel erfahren Sie, warum Maschinenschwingungen im Gerichtsverfahren stets problematisch und eine „besondere Thematik“ sind.
Vibrationen können eine Vielzahl von Auswirkungen haben, von der Geräuschentwicklung bis hin zur Beschädigung von Anlagen und Maschinen. Dieser Artikel geht kurz auf strukturdynamische Grundlagen ein und erläutert reale Probleme in Rechtsstreitigkeiten. Schwingungen im Gerichtsverfahren sind häufig ein Bestandteil des gerichtlichen Beweisbeschlusses. Diese Thematik führt fast immer zu „interessanten Formulierungen“ in Bezug auf Vibrationen.
Darüber hinaus werden besondere Aspekte aufgezeigt, die in der Realität in Gerichtsverfahren bei Schwingungen von Maschinen ein großes Problem vor den zuständigen Gericht darstellen: Die Beweispflicht der beweispflichtigen Partei und Tatsachenfeststellungen von gerichtlichen Sachverständigen in solchen Auseinandersetzungen bei Schwingungen.
Tauchen Sie mit ein in die faszinierende Welt der Maschinenschwingungen, Resonanzen und Vibrationen im Maschinenbau. Erfahren Sie, warum dieses Thema manchmal zu einer juristischen Arena werden kann.
Kurze Einführung in Maschinenschwingungen
Eine äußerst kurze Einführung ist nötig, um auch technischen Laien einen ganz, ganz kleinen Eindruck von der zugrunde liegenden Physik und Mathematik und somit der Komplexität des Themas „Schwingungen“ ansatzweise zu vermitteln.
Abbildung 1 zeigt das Ergebnis der Simulation eines nichtlinearen mathematischen Modells, welches wesentliche physikalische Eigenschaften eines Pkw-Scheibenwischers abbildet.
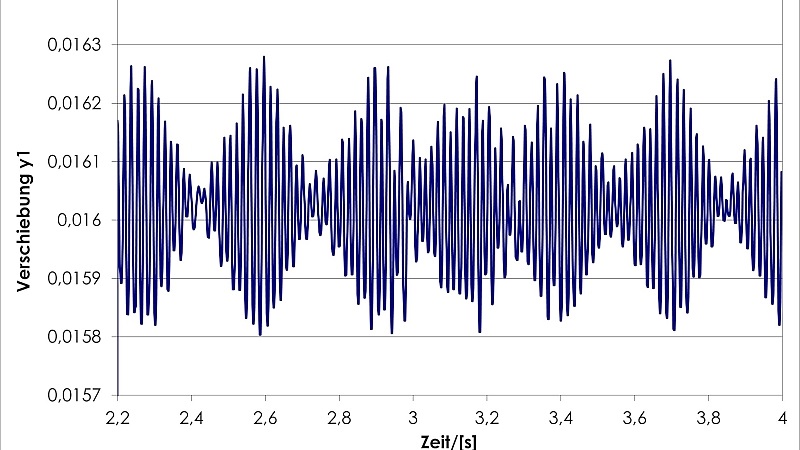
Die Abbildung 1 zeigt auch für Laien einen Schwingungsverlauf über der Zeit, wo sich eindeutig „Wiederholungen“ erkennen lassen. Somit ist dies ein gutes Beispiel für die einfache Definition einer Schwingung.
Unter einer Schwingung versteht man einen Vorgang, bei dem sich
die interessierende Größe (Weg, Geschwindigkeit) mit der Zeit so ändert, dass bestimmte Merkmale wiederkehren.
Welche Schwingungen gibt es?
Man unterscheidet verschiedene unterschiedlichen Formen von Schwingungen, wie zum Beispiel
- freie Schwingungen,
- erzwungene Schwingungen,
- parametererregte Schwingungen,
- selbsterregte Schwingungen usw. .
Dieser kurze Artikel kann selbstverständlich nicht detailliert auf die Unterschiede der verschiedenen Schwingungsformen eingehen. Vielmehr sollen wesentliche Merkmale eines schwingungsfähigen Systems mit möglichst einfachen Worten erläutert werden.
Schwingungsfähige Systeme sind
physikalisch immer gleich aufgebaut
und lassen sich allgemein mathematisch immer beschreiben über
- Masse,
- Steifigkeit,
- Dämpfung und gegebenenfalls
- die Anregung des Systems,
wenn es sich um kein freies System handelt.
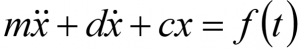
Gleichung 1 beschreibt nun eine erzwungene Schwingung für einen gedämpften 1-Massen-Schwinger. Es ist ein äußerst einfaches Beispiel. Die Eigenfrequenz dieses Systems lässt sich einfach ermitteln aus
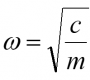
Dabei sind:
m:
d:
c:
f(t):
x**,x*,x:
(schwingende) Masse;
Dämpfung;
Steifigkeit;
Anregung des Schwingungssystems;
Beschleinigung, Geschwindigkeit, Weg.
Resonanz
Abbildung 2 zeigt rein exemplarisch unterschiedliche Vergrößerungsfunktionen (Resonanzkurven).
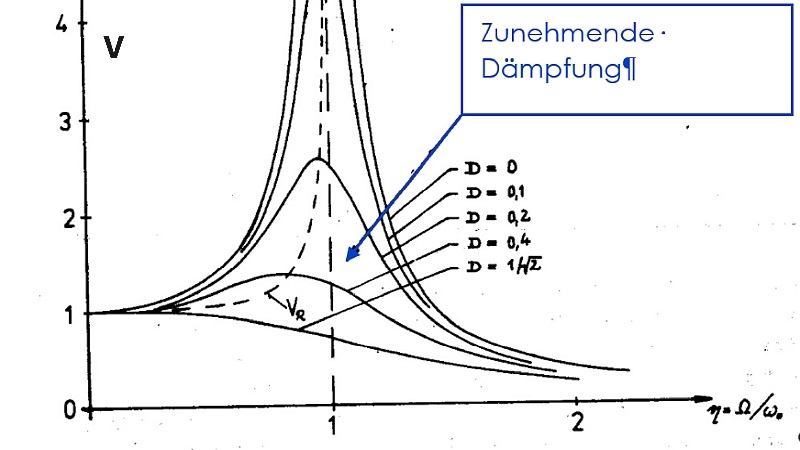
Bei einem Schwingungssystem steigt die Schwingungsantwort umso mehr an, je näher sich die Erregerfrequenz der bzw. einer Eigenfrequenz des Schwingungssystems nähert. Diesen Zusammenhang stellt – rein exemplarisch – Abbildung 2 dar.
Im „ungedämpften“ Fall wird bei der Anregung des Schwingungssystems mit der Eigenfrequenz die Schwingungsantwort sogar „unendlich“ groß. Bei „gedämpften“ Systemen steigt die Schwingungsantwort ebenfalls signifikant an. Rein mathematisch erreicht sie „endliche“ Werte. Je größer die Dämpfung des Systems ist, desto geringer fällt der Anstieg in der Resonanzspitze (auch Resonanzüberhöhung genannt) aus.
Im Allgemeinen versteht man unter
Resonanz die Übereinstimmung von Eigenfrequenz und Störfrequenz.
An dieser Stelle muss noch erwähnt werden, dass beim gedämpften System die Resonanzfrequenz nicht mit der Resonanzfrequenz des ungedämpften Schwingers zusammenfällt.
Reale Schwingungssysteme
Der wesentliche Unterschied zwischen theoretischen Modellen mit wenigen Freiheitsgraden und der Realität ist, dass reale Schwingungssysteme über eine
unendliche Anzahl von Freiheitsgraden
verfügen. Daraus resultieren auch
unendlich viele Eigenfrequenzen sowie Eigenformen, die sich stets in der Schwingung überlagern.
Analytische Approximation des Schwingungssystems
Bei der analytischen Erfassung von Schwingungssystemen bemüht man sich, „lediglich“ die wesentlichen Eigenschaften, welche physikalisch „verstanden“ werden wollen, zu untersuchen. Das macht den Aufwand erträglich und mit heutigen Methoden auch analysierbar. Zunächst wird ein sogenanntes physikalisches Ersatzmodell erstellt. Daraus wird schließlich das mathematische Modell abgeleitet, welches dann analysiert werden kann. Das erfolgt schließlich numerisch. Allgemein liegen bei diesem Vorgehen dann „nur noch“ n Freiheitsgrade vor. Gleichung 2 verdeutlicht, wie sich selbst bei
realen Systeme exorbitant große Gleichungssysteme ergeben.
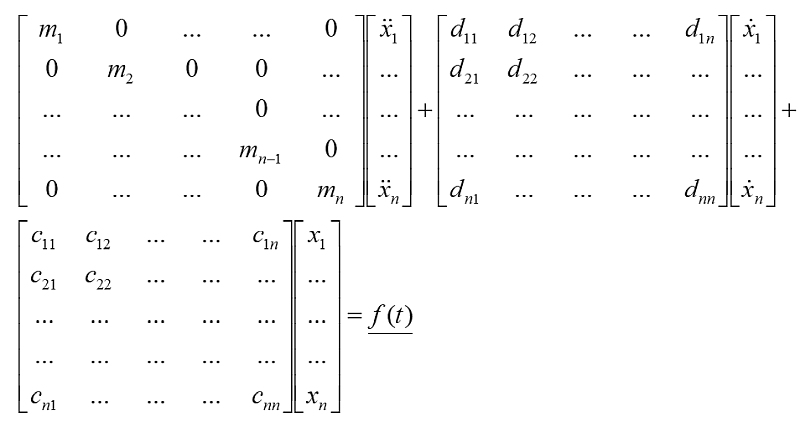
Gleichung 2 lässt sich allgemein in folgender Form für n Freiheitsgrade formulieren:
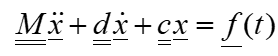
An dieser Stelle dürfte auch dem schwingungstechnischen Laien klar sein, dass
derartige reale Systeme nicht „einfach so“ durch Draufschauen oder technisches „Gefühl“ lösbar sind.
Jegliche „schnelle“ von „Experten“ und manchmal auch „kreativen“ Juristen in den Raum gestellte Hypothese, die für eine schwingungstechnische Schadenursache als „schnelle Erklärung“ herangezogen wird, bedarf
selbstverständlich der technischen, experimentellen und/oder der mathematisch-physikalischen Nachweisführung.
Eigenschwingungen
Wird ein System aus einer Gleichgewichtslage ausgelenkt und sich selbst überlassen, so führt es sogenannte „freie Schwingungen“ aus. Das bedeutet, dass die rechte Seite in der Gleichung 2 bzw. Gleichung 3 gleich Null gesetzt wird.
Die freien Schwingungen sind immer eine Überlagerung der verschiedenen Eigenschwingungen des Systems, die wiederum durch die Eigenfrequenzen und die Eigenformen charakterisiert werden.
Es ist daher von fundamentaler Bedeutung,
- die Eigenfrequenzen und die
- dazugehörigen Eigenformen eines schwingungsfähigen Systems zu kennen,
wenn man diese Schwingungen
- verstehen,
- erklären und
- beeinflussen will.
Eigenwerte / Eigenfrequenzen
Die Differenzialgleichung nach Gleichung 3 löst man allgemein mit dem Ansatz:
Damit gelten für die Geschwindigkeiten sowie die Beschleunigungen:
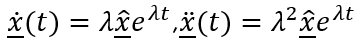
Setzt man nun die Beziehungen nach Gleichung 4 in Gleichung 3 ein, erhält man allgemein:
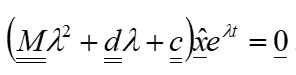
Da die e-Funktion niemals gleich null sein kann, kann die Gleichung 5 reduziert werden auf die Lösung:
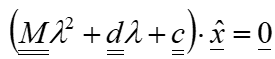
Die Gleichung 6 wird nur dann erfüllt, wenn der Ausdruck in der Klammer identisch null ist oder der Eigenvektor. Da letzteres die triviale Lösung ist, welche der statischen Gleichgewichtslage entspricht, die jedoch im dynamischen Fall nicht interessiert, müssen Lösungen gefunden werden, sodass der Klammerausdruck in Gleichung 6 identisch null wird.
Dies ist dann der Fall, wenn die Koeffizientendeterminante dieses Ausdruckes nach Gleichung 7 gleich null wird:
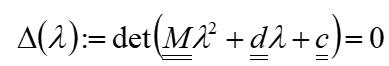
Für reale Probleme ist so etwas
nur mit numerischen Verfahren möglich,
nachdem zunächst das physikalische Modell erstellt und aus diesem das mathematische Modell abgeleitet wurde.
Dies ist zeitaufwändig und erfordert Know-how.
Die n Nullstellen der Lösungen nach Gleichung 7 sind die sogenannten Eigenwerte. Die Eigenfrequenzen des Schwingungssystems lassen sich aus den Eigenwerten ableiten.
Eigenschwingungsformen / Eigenformen
Mit den Lösungen nach Gleichung 7 können nun die Eigenschwingungsformen nach Gleichung 6 bestimmt werden. Wie der Name es schon ausdrückt, sind
Eigenschwingungsformen nur ihrer Form und nicht der Größe nach definiert.
Auch dies lässt sich allgemein an der Gleichung 6 ablesen. Wir haben ein System mit n Freiheitsgraden. Wir benötigen die Lösung nach Gleichung 6. Dazu werden zunächst die Eigenwerte bestimmt.
Nun interessiert aber noch die Eigenschwingungsform. Das bedeutet konkret, dass (n+1) Informationen benötigt werden. Für die Lösung stehen aber nur n Gleichungen zur Verfügung.
Zur Lösung wird daher eine Stelle des Eigenvektors (Eigenform) vorgegeben und der Rest darauf basierend mathematisch ermittelt. Deswegen ist die Eigenschwingungsform nur der Form und nicht der Größe nach definiert.
Man erhält somit n Eigenvektoren.
Allgemeine Lösung von Schwingungen
Man erhält also als allgemeine Lösung der Schwingung für Freiheitsgrade des Systems in Abhängigkeit der Zeit folgende Lösung:
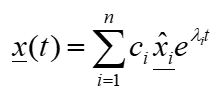
Die Koeffizienten c_i ergeben sich aus den Anfangsbedingungen.
Zusammenfassung für Maschinenschwingungen und Vibrationen
Nachdem nun die doch sehr komplexen Zusammenhänge bei realen Schwingungssystemen – hoffentlich einfach und verständlich – in wirklich sehr wenigen Worten erläutert wurden, ist klar, dass Schwingungstechnik schwierig und alles andere als „auf den ersten Blick“ zu verstehen ist.
Wichtig ist:
Jede Schwingungsproblematik ist individuell zu betrachten. Eine Lösung ist nicht durch „einfaches Daraufschauen“ möglich, weder bei Schwingungen im Gerichtsverfahren noch bei der Prüfung von Vibrationen bzw. Maschinenschwingungen im Parteiauftrag.
Produkthaftung bei Maschinenschwingungen und Vibrationen
Das Thema Produkthaftung bei Produktfehlern nach dem Produkthaftungsgesetz (ProdHaftG) wurde bereits in dem Artikel „Produkthaftung bei Maschinen durch Produktfehler“ ausführlich diskutiert.
Technischer Produktfehler "Maschinenschwingungen"
Sofern eine technische Problematik hinsichtlich der Vibrationen im Maschinenbau und Anlagenbau bei Maschinenschwingungen bestätigt werden kann, handelt es sich primär um folgende technische Fehlertypen:
- Konstruktionsfehler und
- Fabrikationsfehler bzw. Installationsfehler.
Konstruktionsfehler im Fall von Schwingungen im Gerichtsverfahren
Die Definition besagt, dass ein Konstruktionsfehler nur vorliegt, wenn schon bei der Planung des Produkts gegen technische Erkenntnisse verstoßen wird. Der
Fehler liegt zeitlich also vor der Herstellung
und ist dann auch für die komplette Produktionsserie typisch.
Wenn es also tatsächlich eine Produktserie gibt, wird es im Rahmen von Tatsachenfeststellungen an einem Referenzprodukt technisch möglich sein, einen solchen Konstruktionsfehler im Fall von Maschinenschwingungen technisch gerichtsfest nachzuweisen.
Schwieriger gestaltet sich, wenn eine einzelne Maschine zerstört wurde und man dann einen Schaden durch Schwingungen der Maschine nachweisen möchte. In solchen Fällen ist in der Regel
technisch nicht mehr möglich, den Nachweis zu führen.
Fabrikationsfehler bzw. Installationsfehler bei Schäden durch Schwingungen
Fabrikationsfehler beziehen sich auf Fehler, die
während des Herstellungsprozesses
auftreten. Bei Vibrationen, Resonanzen und Schwingungen im Gerichtsverfahren bedeutet das dann in der Regel die
fehlerhafte Montage.
Fehlerhafte Montage führt bei sich bewegenden Maschinen sehr häufig zu veränderten „Steifigkeiten“ des Schwingungssystems. Dies beeinflusst bei den zugrunde liegenden Gleichungen in jedem Fall die Steifigkeitsmatrix c nach Gleichung 3.
Das Problem ist bei einzelnen Maschinen, die keine Serienprodukte sind und in geringen Stückzahlen hergestellt werden:
Wie will man dies nachweisen, wenn man als Partei im Gerichtsverfahren beweispflichtig ist?
Beispiele für Maschinenschwingungen
Es gibt zahlreiche Schwingungsbeispiele, die ich präsentieren könnte. Ich habe lediglich zwei ausgewählt, die klassische Situationen bei Maschinenschwingungen und insbesondere Schwingungen im Gerichtsverfahren exemplarisch zeigen.
Vibrationen einer Pumpe
Eine Pumpe, die in Bild 2 bereits ausgebaut ist, soll zu erheblichen Schwingungen geneigt haben, nachdem sie repariert wurde.

Die große Problematik in einer Situation nach Bild 2 ist, dass es weder als Parteisachverständiger noch als Gerichtssachverständiger im Auftrag des Gerichts bei einem „Gerichtsverfahren Schwingungen“ möglich ist, überhaupt etwas festzustellen, wenn bereits demontiert wurde.
Warum ist das so?
Das Schwingungsverhalten von Strukturen hängt sehr von den Anbindungsrandbedingungen („Lagerungen“) ab. Wenn sich die schwingenden Massen M nach Gleichung 3 nicht ändern, was so gut wie nie mit Ausnahme des Beispiels nach Bild 1 vorfällt, bleiben als Einflüsse nur noch
- die Änderung der Dämpfung d,
- der Steifigkeit c oder
- der Anregung f(t) des Systems übrig,
um einen Schaden technisch zu erklären. Die entscheidende Frage einer Situation nach Bild 2 ist jedoch:
Wie soll ein Sachverständiger eine Ursache finden, wenn das System nicht mehr im installierten und diskutierten bzw. bemängelten Zustand existiert?
Die technische Antwort ist sehr einfach: Es ist nicht mehr möglich!
Maschinenschwingungen durch Unwucht
Bild 3 zeigt einen weiteren Schaden durch eine Schwingungsproblematik. Es war ein großer Schaden, den man beim Betrachten von Bild 3 nur hinsichtlich seiner Dimension kaum erahnen kann.

Die Anlage wurde schwingungstechnisch dauerhaft überwacht. Die Betreiberin nahm nach einiger Zeit im Betrieb hörbare Geräusche wahr und stellte auch fest, dass sich gemessene Schwingwege vergrößert hatten.
Die Herstellerin ignorierte die Informationen der Betreiberin, da die gemessenen Schwingwege nach wie vor in die DIN-Norm „passten“.
Normalerweise ist es bei völlig zerstörten Maschinen so gut wie gar nicht mehr möglich, die Ursache des Schadens exakt nachzuweisen, insbesondere bei der Hypothese „Maschinenschwingungen“.
Im vorliegenden Fall gab es jedoch ausführliche Aufzeichnungen der Betriebsparameter. Man konnte sehen, dass sich das System in einer relativ kurzen Zeitspanne aufgeschwungen hatte. Insbesondere bei rotierenden Strukturen ist dies immer ein Hinweis auf eine Unwucht.
Die Tatsache, dass es im vorliegenden Fall ausführliche Aufzeichnungen der Betriebsparameter gab, konnte den Fall zwar prinzipiell erklären.
Entscheidend für die zu klärende haftungsrechtliche Problematik sind jedoch stets die Fragen:
- Was ist bzw. war die Schadenursache?
- Wer bzw. welche Partei ist dafür verantwortlich?
Die Klärung dieser Frage kann bei technischen Schäden auch im Fall von Maschinenschwingungen einige Juristen, Versicherungen und auch Gerichte in Einzelfällen jahrelang beschäftigen, wenn eine Thematik nicht auf den sprichwörtlichen Punkt gebracht wird.
Häufig wird dann im Laufe der Jahre über mögliche technische Szenarien und damit verbundene Verantwortlichkeiten unter den Beteiligten juristisch „philosophiert“.
Die wichtige Frage nach der technischen Schadenursache ist normalerweise mit den aussagefähigen und aufgezeichneten Betriebsparametern
noch nicht beantwortet.
Im vorliegenden Fall konnte jedoch festgestellt werden, dass sich aufgrund einer fehlerhaften Schweißnaht ein 160°-Segment aus einem Laufrad gelöst hatte. Das war der Grund für die Unwucht. Damit konnte dieser Schwingungsschaden auch ohne Gerichtsverfahren geklärt werden.
Schwingungen im Gerichtsverfahren
In einem Gerichtsverfahren wurde behauptet, dass „auffällige Vibrationen“ an einem Generator festgestellt wurden. Maßgeblich für die Klage wegen Maschinenschwingungen war die Schwingungsmessung in einem Punkt.

Natürlich ist es möglich, Maschinenschwingungen in einem Punkt zu messen. Wenn man zum Beispiel technische Änderungen am System durchführt sowie an ein und demselben Punkt die Vergleichsmessungen vornimmt, wird man sehr wahrscheinlich im Vergleich der Messergebnisse auch Änderungen in der Schwingungsantwort erkennen können.
Für Vergleiche ist es aus der technischen Kategorie „o. k.“. Für absolute Aussagen sind punktuelle Messungen an Strukturen riskant, weil wesentliche Informationen verloren gehen können.
Ich verweise auf den Abschnitt 6.1.1.1 „Knotenlinien“. Wird entlang einer Knotenlinie einer die Anregung dominierenden Eigenschwingungsform punktuell gemessen, misst man „irgendetwas“ oder theoretisch sogar überhaupt nichts. Auf jeden Fall misst man in einem solchen Fall technisch nichts Sinnvolles.
Maschinenschwingungen im gerichtlichen Beweisbeschluss
Ein gerichtlicher Beweisbeschluss ist eine richterliche Anordnung, die im Rahmen eines Gerichtsverfahrens erlassen wird und darauf abzielt, die Beweisaufnahme zu regeln. Der Beweisbeschluss dient dazu, sicherzustellen, dass alle relevanten Tatsachen und Umstände im Verlauf eines Rechtsstreits ermittelt und gewürdigt werden können.
Gerichtssachverständige sind an den Beweisbeschluss gebunden. Die dort gestellten Fragen sind entsprechend zu beantworten.
Die Gerichte übernehmen Formulierungen der Parteien aus den Schriftsätzen der Juristen häufig mehr oder weniger exakt in den Beweisbeschluss des Gerichtes. Es ist auch nachvollziehbar, denn schließlich sind Juristen die Fachleute des Rechts und nicht jeder einzelnen Disziplin, aus welcher einer Problematik kommt, über welche das Gericht eine Entscheidung im Rahmen der Klage zu treffen hat.
Das führt im Bereich von Schwingungen im Gerichtsverfahren regelmäßig zu extrem unpräzisen technischen Fragestellungen. Die folgenden zwei Beispiele sollen einen Eindruck vermitteln. Ich könnte an dieser Stelle etliche Beispiele aufführen.
Beispiel 1 für gerichtliche Beweisbeschlüsse bei Maschinenschwingungen
Abbildung 4 zeigt den Beweisbeschluss für einen Fall von Schwingungen im Gerichtsverfahren.

Bei dem Beispiel nach Abbildung 4 stellen sich dem professionellen Sachverständigen aus dem Bereich der Maschinenschwingungen sofort die technischen Fragen:
- Was sind denn „auffällige Vibrationen“?
- Wie wurden diese Maschinenschwingungen ermittelt?
- An welcher Stelle wurden diese Vibrationen festgestellt oder wo sollen die Schwingungen im Gerichtsverfahren festgestellt werden?
Darüber hinaus stellt sich bei so einem Beweisbeschluss die Frage, wie ein Gerichtssachverständiger feststellen soll, was angeblich irgendwelche Mitarbeiter zwischenzeitlich möglicherweise mitgeteilt haben. Zeugenvernehmung ist die Aufgabe des zuständigen Gerichts. Gerichtssachverständige dürfen keine Zeugen vernehmen. Sie sind vielmehr Experten ihres speziellen Fachgebietes und in diesem Fachgebiet die Helfer des Gerichts.
Beispiel 2 für gerichtliche Beweibeschlüsse bei Vibrationen
Aus dem Beispiel Abbildung 5 geht hervor, dass die Austragsschnecken gar nicht mehr im zu beurteilenden System zum Zeitpunkt des Gerichtsverfahrens verbaut sind.

Ein Richter hat keine Chance zu erkennen, dass so etwas im Fall von Schwingungen bei Maschinen nicht mehr überprüft werden kann.
Unklar ist für mich bei derartigen Beweisbeschlüssen immer, wieso Parteien unter solchen technischen Randbedingungen in einen Rechtsstreit gehen. Es muss doch auf der Seite der Partei kompetente technische Experten geben, die den Parteijuristen entsprechende technische Hinweise geben sollten. Die entscheidende Frage für den gerichtlichen Sachverständigen ist in einem Fall nach Abbildung 5:
Wie soll diese Frage beantwortet werden? Es geht nicht.
Warum ist das Schwingungssystem so wichtig?
Es ist von fundamentaler Wichtigkeit,
- die Eigenfrequenzen und
- die Eigenschwingungsformen
eines Schwingungssystems bei Maschinenschwingungen zu kennen oder festzustellen. Ein Sachverständiger muss also das Schwingungssystem verstehen, um substantiierte Feststellungen bei Schwingungen im Gerichtsverfahren zu ermöglichen.
Unabhängig von der absoluten Größe der Anregungen des Systems („Erregungen“) und Dämpfungen, ist die Kenntnis der wesentlichen Eigenfrequenzen und Eigenformen sehr hilfreich, um das dynamische Verhalten bewerten zu können.
Es gibt Messverfahren, um die Eigenschwingungsformen bei realen Strukturen darstellen zu können.
Wenn man die Konstruktionsdaten zur Verfügung hat und diese mit der in der Realität umgesetzten Struktur abgleicht, kann man reale Strukturen auch verhältnismäßig einfach – allerdings mit großen Zeitaufwand – mittels geeigneter Software untersuchen.
Je nach Diskretisierung der Struktur sind dann die Analyseergebnisse zum Beispiel mit der Methode der finiten Elemente (FEM) bezüglich der Eigenschwingungsformen sehr genau. Bei den dann ermittelten Eigenfrequenzen gibt es
immer wieder teilweise deutliche Abweichungen zur Realität.
Wesentlich ist jedoch die Kenntnis der Eigenschwingungsformen, weil man dann weiß, welche „Form“ man gegebenenfalls durch „welche“ Eingriffe in die Struktur in Richtung gewünschter Frequenzbereiche verschieben muss, um unerwünschte Effekte zu vermeiden.
Dabei muss berücksichtig werden:
So etwas kann kein Experte durch Draufsehen schaffen
und insbesondere dann nicht, wenn
- der Schaden schon passiert und
- die Strukturen demontiert oder
- zerstört sind.
In all diesen Fällen sind wesentliche technische Informationen verloren gegangen. Das ist bei Schwingungen im Gerichtsverfahren
immer mit einem Nachteil für die beweispflichtige Partei verbunden.
Warum das Schwingungssystem so wichtig ist, soll das folgende simple Beispiel illustrieren.
Einfluss von Randbedingungen bei Schwingungen an einem einfachen Beispiel
In der Abbildung 6 sieht man in der Draufsicht zwei einfache rechteckige Platten, die in einer FEM-Analyse in einem sogenannten Schalenmodell abgebildet wurden.
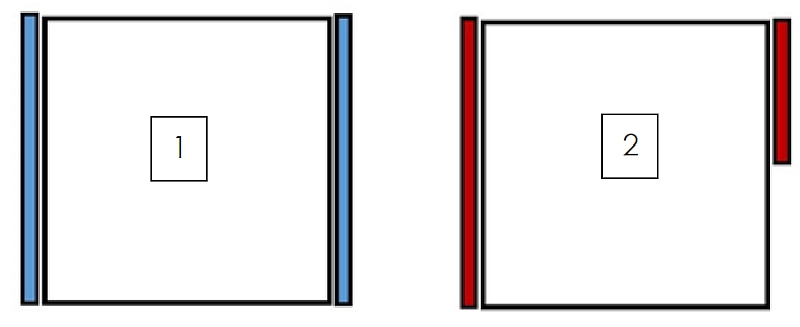
Mit der Bezeichnung „1“, „links“ in der Abbildung 6, sind die beiden hellblauen Ränder komplett blockiert („Randbedingung 1“ in Tabelle 1). Verschiebungen sind entlang diese blauen Ränder ausgeschlossen.
Mit der Bezeichnung „2“, „rechts“ in der Abbildung 6, sind nur die roten Ränder komplett blockiert. Verschiebungen sind „rechts unten“ möglich („Randbedingung 2“ in Tabelle 1).
Eigenschwingungsformen ("Moden")
Abbildung 7 zeigt den Vergleich der jeweils ersten Eigenform. Im Fall „1“ über beide komplett blockierte Ränder, ergibt sich der klassische Schwingungsbauch, der bei Symmetrie exakt mittig verläuft.
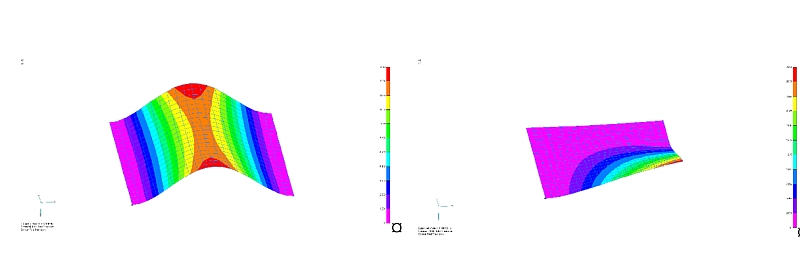
Im Fall „2“ schwingt lediglich der freigelassene Randbereich. Die zugehörige Frequenz ist um ganze 2 Hz niedriger als im Fall „1“ mit der Einspannung über den kompletten Rand.
Knotenlinien bei Schwingungen, Vibrationen, Resonanzen
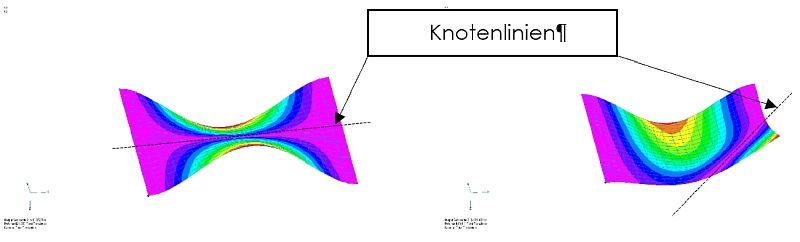
Abbildung 8 zeigt ebenfalls signifikante Unterschiede in der Eigenschwingungsform und selbstverständlich in der Eigenfrequenz. In beiden Fällen erkennt man die sogenannten Knotenlinien.
Knotenlinien bedeuten bei zweidimensionalen Strukturen, dass Eigenschwingungsformen entlang dieser Linien
„trotz Schwingung“ in Ruhe sind und es auch bleiben.
Man sieht im linken Teil der Abbildung 8 („Randbedingung 1“), dass hier die erwartete Symmetrie vorliegt. In dem Fall mit dem nur teilweise eingespannten Rand, ergibt sich eine Eigenschwingungsform, die sich als Kombination aus dem bei Symmetrie vorhandenen Schwingungsbauch nach Abbildung 7 („links“) und dem Schwingungsverhalten nach Abbildung 7 („rechts“) ergibt.
| Mode | „1“ | „2“ |
|---|---|---|
| 1 | 3,47 Hz | 1,40 Hz |
| 2 | 4,11 Hz | 3,41 Hz |
| 3 | 6,73 Hz | 4,45 Hz |
| 4 | 9,58 Hz | 5,6 Hz |
Tabelle 1: Einfluss von Randbedingungen.
Schaut man sich nun die ermittelten Eigenfrequenzen 3 und 4 nach Tabelle 1 an, so erkennt man auch hier deutliche Unterschiede.
Dieses Beispiel soll verdeutlichen, dass Randbedingungen, wie zum Beispiel
- Anbindungen,
- Lagerungen,
- Bewegungsmöglichkeiten usw.
das Schwingungsverhalten von Strukturen signifikant beeinflussen.
Diese Veränderung bezieht sich auf die
Eigenfrequenzen und die zu diesen Eigenfrequenzen gehörenden Eigenschwingungsformen („Moden“).
Damit soll an dieser Stelle auch nochmals für den Laien klar und deutlich ausgedrückt werden, dass man wissen muss,
- was man sucht und vor allem
- bei welcher Frequenz,
damit hier technische Rückschlüsse auf Ereignisse gezogen werden können und diese – im Idealfall – zukünftig vermieden werden. Daraus folgt:
Schwingungstechnische Problemstellungen wie Maschinenschwingungen sind daher ein technisch sehr anspruchsvolles Aufgabengebiet für Spezialisten.
Technische Empfehlungen
Die Ausführungen sind nur ein ganz kleiner Ausflug in den faszinierenden Bereich der Schwingungstechnik und schwingungstechnischer Problemstellungen von Maschinen, Anlagen aus dem Maschinenbau.
Ich empfehle dringend, dass sich Parteien genauestens technisch überlegen oder von Schwingungsexperten beraten lassen, inwieweit eine Schwingungsproblematik vorliegen könnte. Danach ist es
wichtig zu prüfen, ob und wenn ja, wie diese auch in einem Rechtsstreit nachgewiesen werden kann.
Wenn eine Partei mit einer technischen Problematik aus dem Bereich der Maschinenschwingungen ein selbstständiges Beweisverfahren oder gar eine Klage in einem Gerichtsverfahren anstrebt, sollte sich die Partei sicher sein, dass Beweise auch im Rechtsstreit erbracht werden können.
Es ist für einen Rechtsanwalt in der Klage oder im selbstständigen Beweisverfahren immer recht einfach, den „Beweis: Sachverständigengutachten“ anzubieten.
Das hilft jedoch nicht weiter, wenn ein gerichtlicher Sachverständiger nichts mehr feststellen kann, weil
- das Schwingungssystem zerstört oder
- bis zum gerichtlichen Ortstermin verändert wurde.
Wenn eine Partei intern oder gar mit Hilfe eines fachlich guten Parteisachverständigen zu der technischen Erkenntnis gelangt sein sollte, dass eine behauptete Problematik mit Maschinenschwingungen auch im Rechtsstreit nachgewiesen werden kann, kann ich nur empfehlen, diesbezügliche Fragen für den Beweisbeschluss
technisch präzise zu formulieren
und dies im Fall von „Schwingungen im Gerichtsverfahren“
nicht Juristen der eigenen Partei
zu überlassen.
Das ist kein Misstrauen gegenüber dem Berufsstand der Rechtsanwälte. Ich habe fantastische Rechtsanwälte kennengelernt. Es ist immer wieder eine Freude, mit juristischen Experten in kniffligen technischen Fällen auf hohem Niveau zusammenzuarbeiten. Juristen sind aber Fachleute des Rechts.
Es dürfte anhand der vorangestellten Ausführungen klar sein, dass Vibrationen ein sehr schwieriges technisches Thema darstellen. Das gilt insbesondere dann, wenn es nötig ist, in einer Rechtsstreitigkeit wegen „Maschinenschwingungen“ etwas nachzuweisen.
Rechtsanwälte können dieses technische Know-how nicht haben. Deswegen ist bei Schwingungen im Gerichtsverfahren immer exzellenter fachlicher Rat auf der Seite der Partei nötig. Grundsätzlich empfehle ich:
Überlegen Sie sich als Partei sehr genau, ob sie im Fall von Maschinenschwingungen ein hohes Prozessrisiko in einem Rechtsstreit eingehen wollen.
Schwingungen im Gerichtsverfahren sind aufgrund der Tatsache, dass das Problem in fast allen Fällen bereits „erledigt“ ist, fast nie nachträglich sicher durch Gerichtssachverständige feststellbar und erklärbar. Es wird immer ungeklärte Aspekte geben. Das ist in Rechtsstreitigkeiten immer hilfreich für die nicht beweispflichtige Partei.
Prozessrisiko für Parteien bei Schwingungen im Gerichtsverfahren
Grundsätzlich besteht in einem Rechtsstreit die Gefahr, dass sich Gerichtssachverständige zu fachlichen Fragen äußern, bei welchen sie die eigene Kompetenz schlichtweg überschätzen.
Insbesondere bei Maschinenschwingungen ist absolutes Know-how in Bezug auf Schwingungen, Vibrationen, Resonanzen und Strukturmechanik sowie Strukturdynamik nötig. Kein Gerichtssachverständiger oder technischer Experte ist bei Maschinenschwingungen in der Lage, „scheinbar“ simple Fragen von den Rechtsanwälten der Parteien, zum Beispiel in Gerichtsverhandlungen, ad hoc zu beantworten.
Das ist auch einfach zu erklären: schaut man sich nur die allgemeine Darstellung eines Differenzialgleichungssystems nach Gleichung 2 an, dürfte auch dem Laien klar sein, dass es völlig utopisch ist, den Einfluss irgendwelcher Parameteränderungen „einfach so“ vorhersagen zu können.
Seien Sie also auf der Hut, wenn ihnen ein technischer Sachverständiger in diesem speziellen Gebiet der Maschinenschwingungen im Gerichtsverfahren oder auch auf der Parteiseite erzählt:
„aufgrund der Erfahrung kann ich Ihnen sagen, dass ….“
Grundsätzlich besteht in einem Rechtsstreit die Gefahr, dass sich Gerichtssachverständige zu fachlichen Fragen äußern, bei welchen sie die eigene Kompetenz schlichtweg überschätzen.
Insbesondere bei Maschinenschwingungen ist absolutes Know-how in Bezug auf Schwingungen, Vibrationen, Resonanzen und Strukturmechanik sowie Strukturdynamik nötig. Kein technischer Sachverständiger oder technischer Experte ist in der Lage, scheinbar simple Fragen von den Rechtsanwälten der Parteien, zum Beispiel in Gerichtsverhandlungen, ad hoc zu beantworten.
Das ist auch einfach zu erklären: schaut man sich nur die allgemeine Darstellung eines Differenzialgleichungssystems nach Gleichung 2 an, dürfte auch dem Laien klar sein, dass es völlig utopisch ist, den Einfluss irgendwelcher Parameteränderungen „einfach so“ vorhersagen zu können.
Seien Sie also auf der Hut, wenn ihnen ein technischer Sachverständiger in diesem speziellen Gebiet der Maschinenschwingungen im Gerichtsverfahren oder auch auf der Parteiseite erzählt:
„aufgrund der Erfahrung kann ich Ihnen sagen, dass ….“
Ich kann Ihnen sagen, dass das
ganz sicher ein Irrglaube, gepaart mit Selbstüberschätzung ist
und bei Maschinenschwingungen, generell bei Vibrationen und natürlich auch bei Schwingungen im Gerichtsverfahren
nicht funktioniert.
Fazit und Schlussgedanken
Maschinenvibrationen können zu rechtlichen Auseinandersetzungen führen, wenn sie als Ursache für Produktfehler (Produkthaftung), Schäden oder gesundheitliche Probleme angesehen werden. In allen Fällen von Maschinenschwingungen ist die Beweislast das entscheidende Thema bei der Klärungen von Schwingungen im Gerichtsverfahren.
Meistens sind in der Realität bei Problemen von Maschinenschwingungen
wesentliche technische Feststellungen bei Schwingungen im Gerichtsverfahren nicht mehr möglich,
weil in der Zwischenzeit
- das schwingende System verändert oder
- die Maschine durch den Schaden zerstört wurde oder aber sonstige
- wesentliche Informationen in Bezug auf Schwingungen vernichtet sind.
Irritierend ist, dass im Allgemeinen viele Menschen sowohl aus dem technischen als auch aus dem nichttechnischen und juristischen Bereich großen Respekt vor der „Statik“ haben. Dies liegt möglicherweise daran, dass man früher oder später auch im Privatleben mit der Statik zum Beispiel beim Bau eines Eigenheimes konfrontiert wird und letztlich zufrieden ist, wenn die „Statik geprüft“ ist. Die Statik ist jedoch im physikalischen Sinn das Abfallprodukt der Schwingungstechnik oder Dynamik. Streicht man aus einem Differentialgleichungssytem nach Gleichung 2 oder Gleichung 3, welches das Schwingungsverhalten charakterisiert, die Beschleunigungen und Geschwindigkeiten, ist man bei der statischen Lösung angelangt.
Insbesondere in Rechtstreitigkeiten ist dokumentiert, dass eines zwischen den Parteien im Regelfall nicht stattfand:
Die Definition klarer technischer Anforderungen einerseits und damit verbunden das detaillierte Verständnis des Schwingungsproblems samt seiner technischen Lösung andererseits.
Es ist vielfach interessant, im Rechtsstreit und nach Kenntnis der Aktenlage zu erfahren, mit wie wenig technischer Information die Parteien schwingungstechnische Zusagen machen oder „glauben“, Probleme mit Maschinenschwingungen technisch lösen zu können.
Schwingungstechnik ist jedoch im Regelfall, äußerst kompliziert, sehr zeitaufwändig und wird von den beteiligten Juristen verständlicherweise natürlich völlig unterschätzt.
Selbstverständlich werden öffentlich bestellte und vereidigte Sachverständige als Spezialisten und technische Experten beratend tätig und können Lösungen hinsichtlich komplexer schwingungstechnischer Problemstellungen erarbeiten. Dies kann jedoch nur im Parteiauftrag zu einem angemessenen Honorar geschehen.
Bei Schwingungen im Gerichtsverfahren kann der gerichtliche Sachverständige nur erläutern, an
welcher Stelle möglicherweise Fehler gemacht wurden,
und wer aus technischer Sicht dafür
- die technische Verantwortung trägt und
- welche Auswirkungen mögliche technische Fehler auf die vereinbarte Leistung hatten.
Ein solches Vorgehen ist in der Regel bei Schwingungen im Gerichtsverfahren möglich, liefert jedoch – verständlicherweise – keine technische Lösung.
Problemstellungen aus den Gebieten der Strukturmechanik und Strukturdynamik mit Fragestellungen zu Rissen, Brüchen, Strukturversagen, Dauerfestigkeit, Schwingungstechnik und Maschinenschwingungen sind in allen Bereichen des Maschinenbaus und Anlagenbaus ein Fall für technische Spezialisten, von denen es verhältnismäßig wenige auf dem Markt gibt. Wesentlich ist in diesem Fachgebiet:
Schnelle Lösungen führen mit an Sicherheit grenzender Wahrscheinlichkeit in eine technische und früher oder später auch in eine juristische Problematik.





