What is this article about?
In the world of machines and technology, vibrations are a ubiquitous phenomenon and also “fascinating” for vibration experts. In this article you will learn why machine vibrations are always problematic and a “special issue” in court proceedings.
Vibrations can have a variety of effects, from noise to damage to equipment and machinery. This article briefly addresses the basics of structural dynamics and explains real problems in legal disputes. Oscillations in court proceedings are often part of the court’s evidentiary decision. This topic almost always leads to “ interesting formulations ” in relation to vibrations.
In addition, special aspects are highlighted that in reality represent a major problem before the responsible court in legal proceedings involving vibrations of machines: the burden of proof on the part of the party obliged to provide evidence and findings of fact by court experts in such disputes involving vibrations.
Immerse yourself in the fascinating world of machine oscillations, resonances and vibrations in mechanical engineering. Learn why this issue can sometimes become a legal arena.
Short introduction to machine vibrations
An extremely short introduction is necessary in order to give even technical laypeople a very, very small impression of the underlying physics and mathematics and thus the complexity of the topic of ” vibrations “.
Figure 1 shows the result of the simulation of a nonlinear mathematical model, which depicts the essential physical properties of a car windshield wiper.
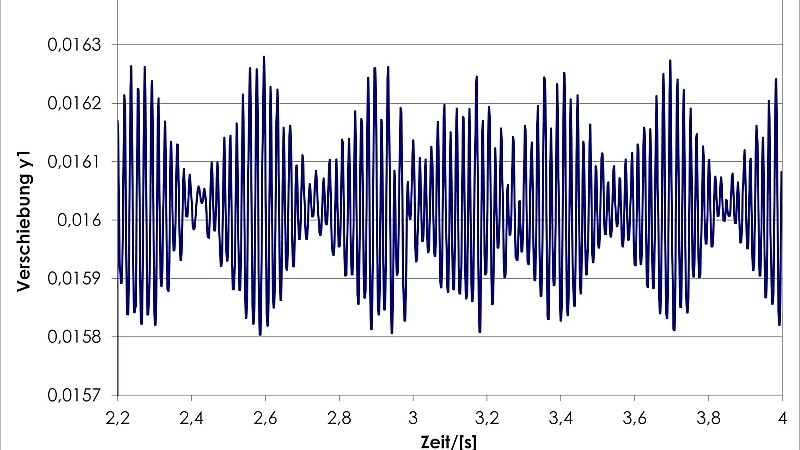
Figure 1 shows, even for laypeople, an oscillation curve over time, where “repetitions” can clearly be seen. So this is a good example of a simple definition of a vibration.
A vibration is a process in which…
the variable of interest (distance, speed) changes over time in such a way that certain features recur.
What vibrations are there?
A distinction is made between various different forms of vibrations, such as:
- free vibrations,
- forced oscillations,
- parameter-excited oscillations,
- self-excited vibrations etc. .
Of course, this short article cannot go into detail about the differences between the various vibration forms. Rather, essential features of an oscillatory system should be explained in the simplest possible terms.
Systems capable of oscillation are
physically always structured the same way
and can generally always be described mathematically
- Dimensions,
- rigidity,
- Damping and if necessary
- the stimulation of the system,
if it is not a free system.
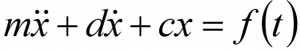
Equation 1 now describes a forced oscillation for a damped 1-mass oscillator. It’s an extremely simple example. The natural frequency of this system can be easily determined from
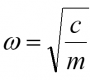
These include:
m:
d:
c:
f(t):
x**,x*,x:
(vibrating) mass;
Damping;
rigidity;
excitation of the vibration system;
Acceleration, speed, distance.
Resonance
Figure 2 shows different magnification functions (resonance curves) purely as examples.
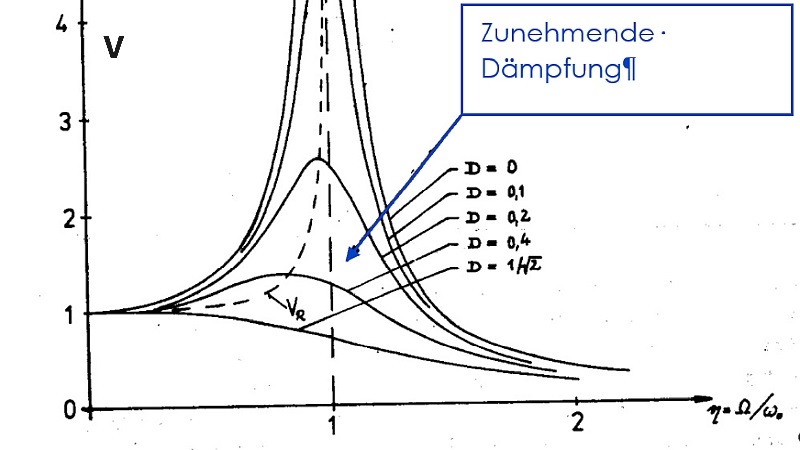
In an oscillation system, the oscillation response increases the closer the excitation frequency approaches the natural frequency of the oscillation system. This connection is shown – purely as an example – in Figure 2.
In the “undamped” case, when the oscillation system is excited at the natural frequency, the oscillation response becomes “infinitely” large. In “damped” systems, the vibration response also increases significantly. Purely mathematically, it reaches “finite” values. The greater the damping of the system, the smaller the increase in the resonance peak (also called resonance peak).
In general, this is understood as:
Resonance is the correspondence between natural frequency and interference frequency.
At this point it must be mentioned that in the damped system the resonance frequency does not coincide with the resonance frequency of the undamped oscillator.
Real vibration systems
The main difference between theoretical models with few degrees of freedom and reality is that real oscillation systems have a
infinite number of degrees of freedom
feature. This also results in
infinitely many natural frequencies and natural shapes that always overlap in the vibration.
Analytical approximation of the vibration system
When analyzing vibration systems, one tries to examine “only” the essential properties that need to be “understood” physically. This makes the effort bearable and can also be analyzed using today’s methods. First, a so-called physical replacement model is created. The mathematical model is ultimately derived from this, which can then be analyzed. This is ultimately done numerically. In general, with this approach there are “only” n degrees of freedom. Equation 2 shows how
Real systems result in exorbitantly large systems of equations.
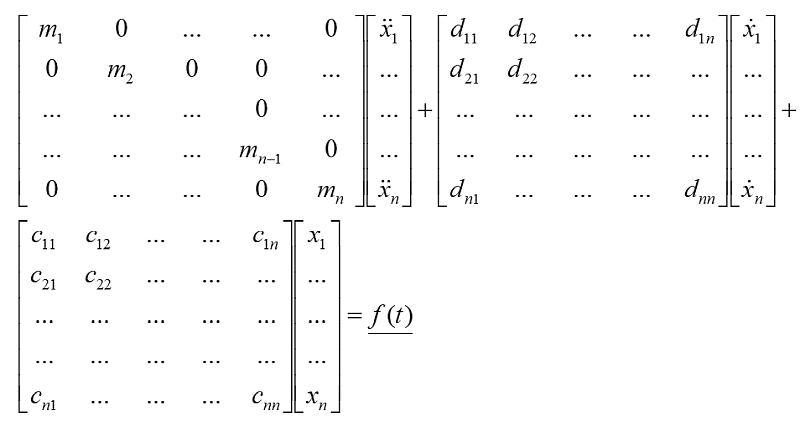
Equation 2 can generally be formulated in the following form for n degrees of freedom:
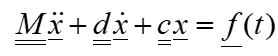
At this point it should also be clear to the vibration technology layman that
Such real systems cannot be solved “just like that” by looking at them or using technical “feeling”.
Any “quick” hypothesis put forward by “experts” and sometimes “creative” lawyers, which is used as a “quick explanation” for a vibration-related cause of damage, is required
of course the technical, experimental and/or mathematical-physical verification.
Natural vibrations
If a system is deflected from a position of equilibrium and left to its own devices, it carries out so-called “ free oscillations ”. This means that the right-hand side in equation 2 or equation 3 is set equal to zero.
The free oscillations are always a superposition of the various natural oscillations of the system, which in turn are characterized by the natural frequencies and the natural shapes.
It is therefore of fundamental importance
- the natural frequencies and the
- to know the associated mode shapes of an oscillatory system ,
when you see these vibrations
- understand,
- explain and
- want to influence.
Eigenvalues / eigenfrequencies
The differential equation according to equation 3 is generally solved using the approach:
The following applies to the speeds and accelerations:
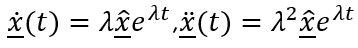
If you now insert the relationships according to equation 4 into equation 3, you generally get:
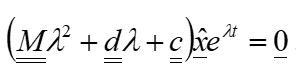
Since the e -function can never be equal to zero, equation 5 can be reduced to the solution:
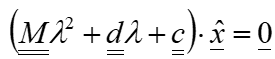
Equation 6 is only satisfied if the expression in the brackets is identically zero or the eigenvector. Since the latter is the trivial solution, which corresponds to the static equilibrium position, but which is not of interest in the dynamic case, solutions must be found so that the expression in brackets in Equation 6 becomes identically zero.
This is the case when the coefficient determinant of this expression becomes zero according to equation 7:
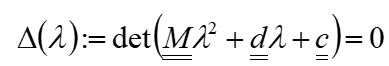
Something like this is for real problems
only possible with numerical methods,
after the physical model has first been created and the mathematical model has been derived from it.
This is time-consuming and requires expertise.
The n zeros of the solutions according to equation 7 are the so-called eigenvalues. The natural frequencies of the vibration system can be derived from the eigenvalues.
Natural vibration shapes/mode shapes
With the solutions according to Equation 7, the natural vibration forms according to Equation 6 can now be determined. As the name suggests, they are
Natural vibration forms are only defined by their shape and not their size.
This can also be generally seen from equation 6. We have a system with n degrees of freedom. We need the solution according to equation 6. To do this, the eigenvalues are first determined.
But now the form of the natural oscillation is of interest. This specifically means that (n+1) information is needed. However, there are only n equations available for the solution.
To solve this, one point of the eigenvector (eigenform) is specified and the rest is determined mathematically based on this. That is why the natural vibration form is only defined by its shape and not its size.
This gives you n eigenvectors.
General solution of oscillations
The following solution is therefore obtained as a general solution of the oscillation for degrees of freedom of the system as a function of time:
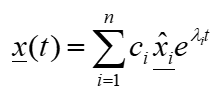
The coefficients c_i result from the initial conditions.
Summary for machine vibrations and vibrations
Now that the very complex relationships in real vibration systems have been explained – hopefully simply and understandably – in very few words, it is clear that vibration technology is difficult and anything but understandable ” at first glance “.
Important:
Each vibration problem must be viewed individually. A solution is not possible by “just looking at it”, neither when it comes to vibrations in court proceedings nor when testing vibrations or machine vibrations on behalf of the party.
Product liability for machine oscillations and vibrations
The topic of product liability for product defects according to the Product Liability Act (ProdHaftG) has already been discussed in detail in the article “ Product liability for machines due to product defects ”.
Technical product error “machine vibrations”
If a technical problem regarding vibrations in mechanical engineering and plant engineering can be confirmed, these are primarily the following technical error types:
- design errors and
- Manufacturing defects or installation errors.
Design defects in case of vibrations in court case
The definition states that a design error only exists if technical knowledge is violated during the planning of the product . The
error therefore predates production
and is then also typical for the entire production series.
If there is actually a product series, it will be technically possible to prove such a design defect in the case of machine vibrations in a court of law as part of factual findings on a reference product.
It is more difficult if an individual machine has been destroyed and you then want to prove damage caused by vibrations of the machine. In such cases, as a rule
it is no longer technically possible to provide proof.
Manufacturing defects or installation errors in the event of damage caused by vibrations
Manufacturing defects refer to defects that
during the manufacturing process
appear. In the case of vibrations, resonances and oscillations in court proceedings, this usually means that
incorrect assembly.
Incorrect assembly often leads to changes in the “stiffness” of the vibration system in moving machines. In the underlying equations, this always influences the stiffness matrix c according to Equation 3.
The problem is with individual machines that are not series products and are manufactured in small quantities:
How do you want to prove this if you as a party in court proceedings have the burden of proof?
Examples of machine vibrations
There are numerous vibration examples that I could present. I have only selected two that exemplify classic situations involving machine vibrations and, in particular, vibrations in court proceedings.
Vibrations of a pump
A pump that has already been removed in Figure 2 is said to have been prone to significant vibrations after it was repaired.

The big problem in a situation according to Figure 2 is that neither as a party expert nor as a court expert commissioned by the court in a “ vibration court case ” is it possible to determine anything at all if the dismantling has already taken place.
Why is that?
The vibration behavior of structures depends very much on the boundary conditions (“supports”). If the oscillating masses M do not change according to Equation 3, which almost never happens with the exception of the example in Figure 1, the only influences left are
- the change in attenuation d ,
- the stiffness c or
- the excitation f(t) of the system remains,
to explain damage technically. However, the crucial question in a situation according to Figure 2 is:
How is an expert supposed to find a cause if the system no longer exists in the installed and discussed or criticized state?
The technical answer is very simple: it is no longer possible!
Machine vibrations due to unbalance
Figure 3 shows further damage caused by a vibration problem. There was a lot of damage, which you can hardly imagine just by looking at picture 3 in terms of its dimensions.

The system was permanently monitored for vibrations. After some time in operation, the operator noticed audible noises and also noticed that measured vibration paths had increased.
The manufacturer ignored the operator’s information because the measured vibration paths still “fit” the DIN standard.
Normally, when machines are completely destroyed, it is almost impossible to prove exactly the cause of the damage, especially in the “ machine vibration ” hypothesis.
However, in this case there were detailed records of the operating parameters. You could see that the system had risen in a relatively short period of time. This is always an indication of imbalance, especially with rotating structures.
The fact that there were detailed records of the operating parameters in this case could in principle explain the case.
However, the following questions are always crucial for the liability law problem to be clarified:
- What is or was the cause of the damage?
- Who or which party is responsible for this?
In the case of technical damage, including machine vibrations, the clarification of this question can keep some lawyers, insurance companies and courts busy for years in individual cases if an issue is not brought to the proverbial point.
Over the years, possible technical scenarios and the associated responsibilities are often legally “philosophized” among those involved.
The important question about the technical cause of damage is usually related to the meaningful and recorded operating parameters
not yet answered.
In the present case, however, it was determined that a 160° segment had come loose from an impeller due to a faulty weld seam. That was the reason for the imbalance. This means that this vibration damage could be resolved without going to court.
Vibrations in the court proceedings
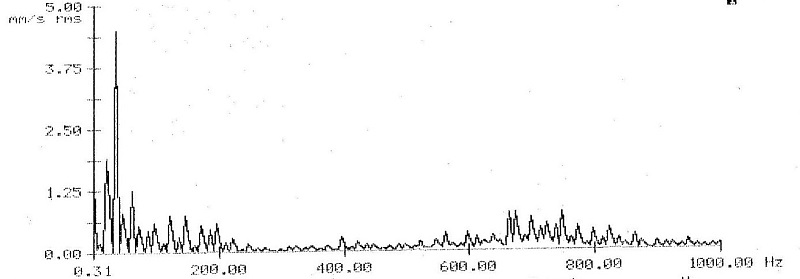
A lawsuit claimed that “noticeable vibrations” were detected on a generator. The vibration measurement in one point was decisive for the lawsuit regarding machine vibrations.

Of course it is possible to measure machine vibrations at one point. For example, if you make technical changes to the system and carry out comparison measurements at one and the same point, you will most likely be able to detect changes in the vibration response when comparing the measurement results.
For comparison purposes it is “ok” from the technical category. For absolute statements, selective measurements on structures are risky because essential information can be lost.
I refer to section 6.1.1.1 “Nodal lines”. If you measure points along a nodal line of a form of natural oscillation that dominates the excitation, you are measuring “something” or, theoretically, nothing at all. In any case, in such a case you are not measuring anything technically meaningful.
Machine vibrations in court evidence
A judicial order for evidence is a judicial order issued as part of a legal proceeding and aimed at regulating the taking of evidence. The evidentiary order serves to ensure that all relevant facts and circumstances can be identified and assessed in the course of a legal dispute.
Court experts are bound by the evidence decision. The questions asked there must be answered accordingly.
The courts often incorporate the parties’ formulations from the lawyers’ pleadings more or less exactly into the court’s evidentiary decision. It is also understandable because, after all, lawyers are experts in the law and not in every single discipline from which a problem arises on which the court has to make a decision in the context of the lawsuit.
This regularly leads to extremely imprecise technical questions in the area of vibrations in court proceedings. The following two examples should give an impression. I could give a number of examples here.
Example 1 for judicial evidence in the case of machine vibrations
Figure 4 shows the evidentiary decision for a vibration case in court.

In the example shown in Figure 4, the professional expert in the field of machine vibration immediately faces technical questions:
- What are “noticeable vibrations”?
- How were these machine vibrations determined?
- Where were these vibrations detected or where should the vibrations be detected in the legal proceedings?
In addition, such an evidentiary decision raises the question of how a court expert is supposed to determine what any employees may have said in the meantime. Examining witnesses is the task of the responsible court. Court experts are not allowed to examine witnesses. Rather, they are experts in their specific field and the court’s helpers in this field.
Example 2 for court decisions regarding vibrations
The example in Figure 5 shows that the discharge screws are no longer installed in the system being assessed at the time of the legal proceedings.

A judge has no chance of recognizing that something like this can no longer be checked in the case of vibrations in machines.
When it comes to such evidentiary decisions, it is always unclear to me why parties enter into a legal dispute under such technical conditions. There must be competent technical experts on the party’s side who should give the party lawyers appropriate technical advice. The crucial question for the forensic expert in a case according to Figure 5 is:
How should this question be answered? It’s not working.
Why is the vibration system so important?
It is of fundamental importance
- the natural frequencies and
- the natural vibration forms
to know or determine the vibration system in machine vibrations. An expert must therefore understand the vibration system in order to enable substantiated findings regarding vibrations in court proceedings.
Regardless of the absolute magnitude of the system’s excitations (“ excitations ”) and dampings, knowledge of the essential natural frequencies and mode shapes is very helpful in order to be able to evaluate the dynamic behavior.
There are measurement methods that can be used to represent the natural vibration patterns of real structures.
If you have the design data available and compare it with the structure implemented in reality, you can examine real structures relatively easily – albeit with a lot of time – using suitable software.
Depending on the discretization of the structure, the analysis results, for example using the finite element method (FEM), are very precise with regard to the natural vibration forms. The natural frequencies then determined are:
there are always sometimes clear deviations from reality.
However, knowledge of the natural vibration forms is essential because you then know which “shape” you need to shift towards the desired frequency ranges through “which” interventions in the structure in order to avoid undesirable effects.
The following must be taken into account:
No expert can do something like this just by looking at it
and especially not if
- the damage has already happened and
- the structures dismantled or
- are destroyed.
In all of these cases, essential technical information was lost. This is with vibrations in court proceedings
always associated with a disadvantage for the party responsible for providing evidence.
The following simple example will illustrate why the vibration system is so important.
Influence of boundary conditions on vibrations using a simple example
In Figure 6 you can see a top view of two simple rectangular plates that were depicted in a so-called shell model in an FEM analysis.
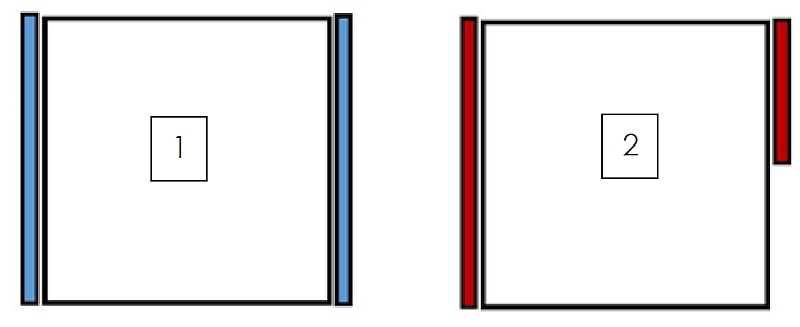
With the label “1”, “left” in Figure 6, the two light blue edges are completely blocked (“boundary condition 1” in Table 1). Shifts are excluded along these blue edges.
With the label “2”, “right” in Figure 6, only the red edges are completely blocked. Shifts are possible “bottom right” (“boundary condition 2” in Table 1).
Natural vibration forms (“modes”)
Figure 7 shows the comparison of the first mode shape. In case “1” with both completely blocked edges, the classic antinode results, which runs exactly in the middle if there is symmetry.
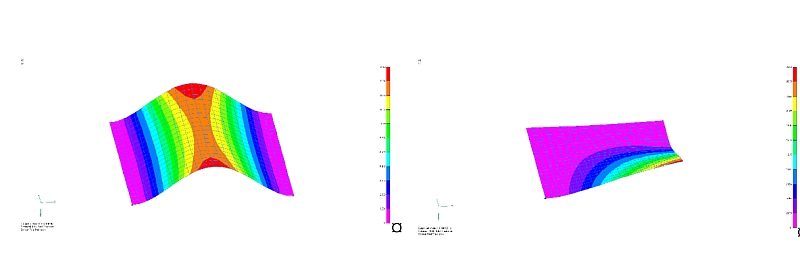
In case “2” only the exposed edge area vibrates. The associated frequency is a full 2 Hz lower than in case “1” with clamping over the entire edge.
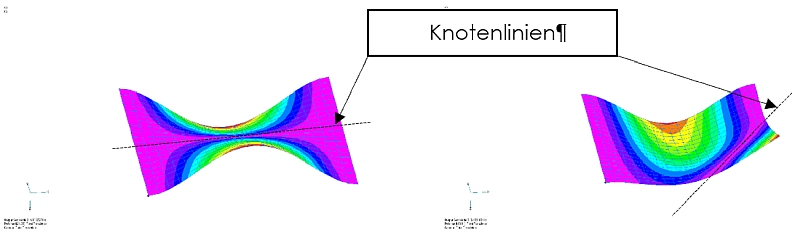
Nodal lines for oscillations, vibrations, resonances
Figure 8 also shows significant differences in the natural vibration shape and of course in the natural frequency. In both cases you can see the so-called nodal lines .
In two-dimensional structures, nodal lines mean that natural vibration forms along these lines
are at rest “despite vibration” and remain so.
You can see in the left part of Figure 8 (“Boundary condition 1”) that the expected symmetry is present here. In the case with the edge only partially clamped, a natural vibration form results, which is a combination of the vibration antinode present in the case of symmetry according to Figure 7 (“left”) and the vibration behavior according to Figure 7 (“right”).
| Mode | “1” | “2” |
|---|---|---|
| 1 | 3,47 Hz | 1,40 Hz |
| 2 | 4,11 Hz | 3,41 Hz |
| 3 | 6,73 Hz | 4,45 Hz |
| 4 | 9,58 Hz | 5,6 Hz |
Table 1: Influence of boundary conditions.
If you now look at the determined natural frequencies 3 and 4 according to Table 1, you can also see clear differences here.
This example is intended to make it clear that boundary conditions such as:
- connections,
- storage,
- movement options, etc.
significantly influence the vibration behavior of structures.
This change refers to the
Natural frequencies and the natural vibration forms (“modes”) associated with these natural frequencies.
This is intended to make it clear again for the layperson at this point that one must know
- what you are looking for and most importantly
- at what frequency,
so that technical conclusions can be drawn about events and – ideally – avoided in the future. It follows:
Vibration problems such as machine vibrations are therefore a technically very demanding area of responsibility for specialists.
Technical recommendations
The explanations are just a very short excursion into the fascinating area of vibration technology and vibration-related problems in machines and systems in mechanical engineering.
I strongly recommend that parties carefully consider the technical aspects or seek advice from vibration experts about the extent to which there may be a vibration problem. After that it is
It is important to check whether and, if so, how this can be proven in a legal dispute.
If a party with a technical problem in the area of machine vibrations wants to initiate an independent evidentiary procedure or even file a lawsuit in court, the party should be sure that evidence can also be provided in the legal dispute.
It is always quite easy for a lawyer to offer “ evidence: expert opinion ” in a lawsuit or in independent evidence proceedings.
However, this doesn’t help if a forensic expert can no longer determine anything, because
- the vibration system is destroyed or
- was changed until the on-site court hearing.
If a party has come to the technical conclusion internally or even with the help of a technically good party expert that an alleged problem with machine vibrations can also be proven in a legal dispute, I can only recommend that relevant questions be included in the evidentiary decision
to be formulated in a technically precise manner
and this in the case of “ vibrations in court proceedings ”
not lawyers from your own party
to leave.
This is not a distrust of the legal profession. I met fantastic lawyers. It is always a pleasure to work with legal experts on tricky technical cases at a high level. But lawyers are experts in the law.
Based on the above, it should be clear that vibrations are a very difficult technical topic. This is particularly true when it is necessary to prove something in a legal dispute over “machine vibrations”.
Lawyers cannot have this technical know-how. That’s why excellent professional advice is always necessary on the party’s side when there are oscillations in court proceedings. Basically I recommend:
As a party, think carefully about whether you want to take a high risk in a legal dispute in the case of machine vibrations.
Due to the fact that the problem has already been “settled” in almost all cases, oscillations in court proceedings can almost never be reliably determined and explained subsequently by court experts. There will always be unexplained aspects. This is always helpful in legal disputes for the party not required to provide evidence.
Litigation risk for parties in the event of fluctuations in the court proceedings
In principle, in a legal dispute there is a risk that court experts will comment on technical questions in which they simply overestimate their own competence.
Particularly when it comes to machine vibrations, absolute know-how in terms of oscillations, vibrations, resonances and structural mechanics as well as structural dynamics is necessary. When it comes to machine vibrations, no court expert or technical expert is able to answer “seemingly” simple questions from the parties’ lawyers on an ad hoc basis, for example in court hearings.
This is also easy to explain: if you just look at the general representation of a system of differential equations according to Equation 2, it should be clear to even the layperson that it is completely utopian to be able to predict the influence of any parameter changes “just like that”.
So be on your guard if a technical expert in this specific area of machine vibration tells you in court proceedings or on the party’s side:
“Based on experience, I can tell you that….”
In principle, in a legal dispute there is a risk that court experts will comment on technical questions in which they simply overestimate their own competence.
Particularly when it comes to machine vibrations, absolute know-how in terms of oscillations, vibrations, resonances and structural mechanics as well as structural dynamics is necessary. No technical expert or technical expert is able to answer seemingly simple questions on an ad hoc basis from the parties’ lawyers, for example in court hearings.
This is also easy to explain: if you just look at the general representation of a system of differential equations according to Equation 2, it should be clear to even the layperson that it is completely utopian to be able to predict the influence of any parameter changes “just like that”.
So be on your guard if a technical expert in this specific area of machine vibration tells you in court proceedings or on the party’s side:
“Based on experience, I can tell you that….”
I can tell you that
is definitely a misconception, coupled with overestimation of oneself
and with machine vibrations, with vibrations in general and of course also with vibrations in court proceedings
doesn’t work.
Conclusion and final thoughts
Machine vibrations can lead to legal disputes if they are viewed as the cause of product defects (product liability), damage or health problems. In all machine vibration cases, the burden of proof is the crucial issue when resolving vibration issues in court proceedings.
Most often in reality there are problems with machine vibrations
Essential technical findings in the case of vibrations are no longer possible in court proceedings,
because in the meantime
- the oscillating system changes or
- the machine was destroyed by the damage or something else
- essential information relating to vibrations has been destroyed.
What is irritating is that in general many people from both the technical and non-technical and legal sectors have great respect for “statics”. This is possibly because sooner or later you will be confronted with statics in your private life, for example when building your own home, and you will ultimately be satisfied when the statics have been checked. However, in the physical sense, statics is the waste product of vibration technology or dynamics. If you delete the accelerations and velocities from a differential equation system according to Equation 2 or Equation 3, which characterizes the vibration behavior, you arrive at the static solution.
In legal disputes in particular, it is documented that one thing usually did not take place between the parties:
The definition of clear technical requirements on the one hand and the associated detailed understanding of the vibration problem and its technical solution on the other.
It is often interesting to find out in the legal dispute and after knowing the file situation how little technical information the parties use to make vibration-related promises or “believe” that they can technically solve problems with machine vibrations.
However, vibration technology is usually extremely complicated, very time-consuming and is understandably overlooked by the lawyers involved of course completely underestimated.
Of course, publicly appointed and sworn experts provide advice as specialists and technical experts and can develop solutions for complex vibration problems. However, this can only be done on behalf of the party for a reasonable fee.
If there are fluctuations in the legal proceedings, the court expert can only explain
where mistakes may have been made,
and who is responsible for it from a technical point of view
- bears technical responsibility and
- what effects possible technical errors had on the agreed service.
Such an approach is usually possible in the event of oscillations in court proceedings, but – understandably – does not provide a technical solution.
Problems from the areas of structural mechanics and structural dynamics with questions about cracks, fractures, structural failure, fatigue strength, vibration technology and machine vibrations are a case for technical specialists in all areas of mechanical and plant engineering, of which there are relatively few on the market. What is essential in this subject area is:
Quick solutions will almost certainly lead to technical and sooner or later legal problems.





